I numeri naturali sono regolati da quattro operazioni fondamentali. Queste sono: addizione, sottrazione, moltiplicazione e divisione.
Le quattro operazioni fondamentali: addizione
La prima della quattro operazioni fondamentali dei numeri naturali è l’addizione. Essa è rappresentata dal simbolo +. I termini dell’addizione si dicono addendi e il risultato si dice somma.

Addizione
Es: 23 + 11 = 34. 23 e 11 sono gli addendi e 34 è la somma dei due addendi.
Lo zero è un numero neutro nell’addizione. Es: 10 + 0 = 10.
Le proprietà dell’addizione
Le proprietà delle operazioni ci permettono di comprendere meglio i meccanismi matematici e di compiere le operazioni più velocemente.
Le proprietà dell’addizione sono:
- Proprietà commutativa: “Cambiando l’ordine degli addendi il risultato non cambia”. Es: a + b = b + a (3 + 4 = 4 + 3).
- Proprietà associativa: “La somma di tre o più addendi non cambia se a due o più di essi si sostituisce la loro somma”. Es: a + b + c = a + (b + c), ovvero 2 + 4 + 3 = 2 + 7.
- Proprietà dissociativa: “La somma di più addendi non cambia se a un addendo ne sostituiscono altri aventi per somma l’addendo sostituito”. Es: a + b = a + (c + d), ovvero 10 + 24 = 10 + 20 + 4.
Le quattro operazioni fondamentali: sottrazione
La sottrazione non è sempre eseguibile e per questo non è un’operazione interna all’insieme N. I termini della sottrazione si dicono minuendo e sottraendo, mentre il risultato si chiama differenza.
Es: 10 – 7 = 3. 10 è il minuendo, 7 è il sottraendo e 3 è il risultato.
Anche in questo caso lo 0 è neutro. Es: 10 – 0 = 10.
Le proprietà della sottrazione
La proprietà della sottrazione è solo una ed è la Proprietà invariantiva. “La differenza di due numeri non cambia se a entrambi si aggiunge o si sottrae lo stesso numero”.
Es: 130 – 120 = 10 / (130 + 10) – (120 + 10) = 10 / (130 – 10) – (120 – 10) = 10.
Le quattro operazioni fondamentali: moltiplicazione
La moltiplicazione può essere scomposta in un’addizione aventi gli addendi tutti uguali (Es: 5 x 3 = 5 + 5 + 5). I termini della moltiplicazione si dicono fattori, mentre il risultato si dice prodotto.

Moltiplicazione
Nella moltiplicazione l’elemento neutro è l’1 (5 x 1= 5). Lo zero, invece, è l’elemento assorbente (5 x 0 = 0).
Le proprietà della moltiplicazione
Le proprietà della moltiplicazione sono:
- Proprietà commutativa: “Cambiando l’ordine dei fattori il prodotto non cambia”. Es: a x b = b x a, ovvero 3 x 5 = 5 x 3.
- Proprietà associativa: “Se sostituisci a due fattori il loro prodotto il risultato non cambia”. Es: a x b x c = a x (b x c), ovvero 3 x 5 x 2 = 3 x (10).
- Proprietà distributiva: “Per moltiplicare una somma o una differenza per un numero si può moltiplicare per quel numero ciascun termine della somma o differenza e poi addizionare o sottrarre i prodotti ottenuti”. Es: (a + b) x c = (a x c) + (b x c), ovvero (6 + 4) x 3 = (6 x 3) + (4 x 3).
- Proprietà dissociativa: “Il prodotto di più fattori non cambia se a un fattore ne sostituiscono altri aventi per prodotto il fattore sostituito”. Es: a x b = a x (c x d), ovvero 5 x 12 = 5 x (3 x 4).
Le quattro operazioni fondamentali: divisione
L’ultima delle operazioni fondamentali è la divisione. I termini della divisione sono il dividendo e il divisore, mentre il risultato è il quoziente o quoto.
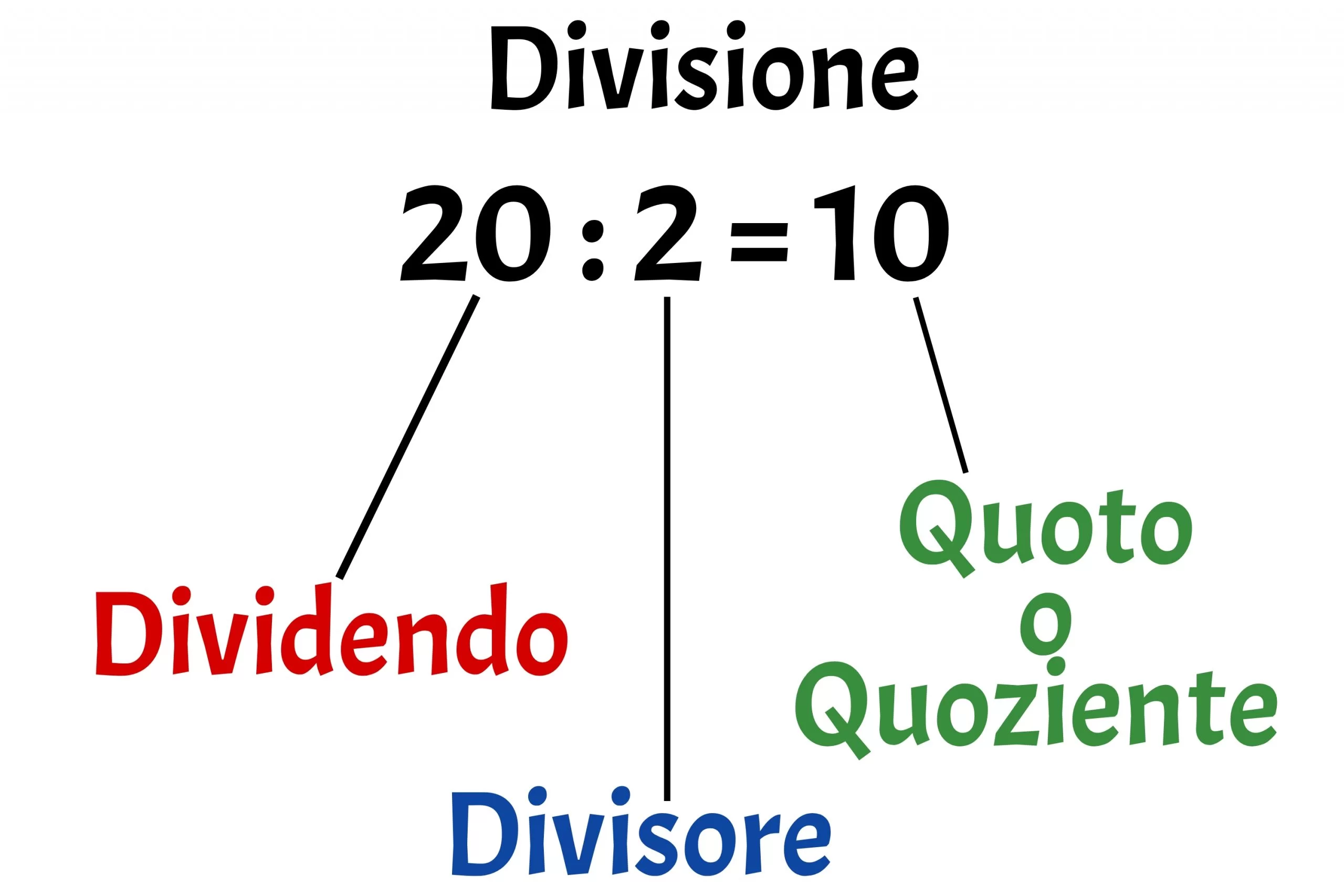
Divisione
Es: 84 : 4 = 21. L’84 è il dividendo, il 4 è il divisore e il 21 è il quoziente o quoto.
Se il dividendo è il numero 0 il risultato è sempre 0. Se il divisore è 0 il risultato è impossibile. Se sia il dividendo che il divisore sono 0 il risultato è indeterminato.
Le proprietà della divisione
Le proprietà della divisione sono:
- Proprietà invariantiva: “Moltiplicando o dividendo, per uno stesso numero diverso da 0 entrambi i termini di una divisione il quoziente non cambia e il resto se c’è, rimane moltiplicato o diviso per quello stesso numero”.
- Proprietà distributiva: “Per dividere una somma o una differenza indicata per un numero, basta dividere ciascun termine per quel numero e addizionare o sottrarre i quozienti ottenuti”.








